PRODUCTOS NOTABLES
Los productos notables son fórmulas matemáticas que representan multiplicaciones de expresiones algebraicas con patrones específicos. Estas fórmulas permiten obtener el resultado de la multiplicación de manera rápida y sencilla, sin necesidad de realizar la multiplicación término a término. Su aprendizaje y dominio son esenciales para simplificar cálculos algebraicos, factorizar polinomios y resolver ecuaciones de forma eficiente.
tipos de productos notables
Binomio al cuadrado
Binomio al cubo
Binomio de Newton
Diferencia de cuadrados
Suma de cubos
Diferencia de cubos
Binomios con término común
Trinomio al cuadrado
Trinomio al cubo
Binomio al cuadrado
Los binomios al cuadrado (o cuadrados de un binomio o binomios cuadrado perfecto), en el caso del cuadrado de una suma del tipo: (a + b)², es igual al cuadrado del primer monomio, más el cuadrado del segundo, más el doble del primero por el segundo.
De este desarrollo resulta el trinomio cuadrado perfecto, que es un producto notable.
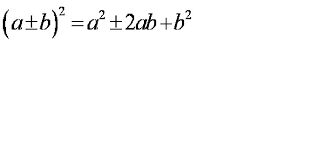
Cuando el binomio al cuadrado es el cuadrado de una diferencia (a – b)² el desarrollo cambia en que hay que ponerle el signo menos al doble del primero por el segundo.
Binomio al cubo
Los binomios al cubo (a + b)³ es igual al cubo del primer término, más el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más el cubo del segundo.
Este desarrollo se llama cuatrinomio cubo perfecto.
El cubo de un binomio se puede escribir así, teniendo en cuenta el desarrollo del binomio al cuadrado:
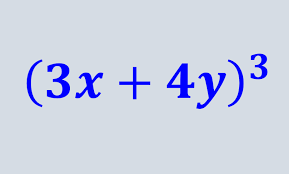
Binomios con termino comun
Binomios con término común se refiere al producto de dos binomios que tienen un término igual en ambos, siendo el otro término diferente.

Esto serían dos ejemplos de binomios con un monomio en común:
El resultado es el cuadrado del término común, más la suma de los monomios no comunes multiplicada por el término común, más el producto de los términos no comunes. Como se ve en este desarrollo, el resultado es un trinomio:
Los binomios con los dos monomios en común, pero uno cambiado de signo, serían un producto notable, en concreto suma por diferencia.
Trinomio al cuadrado

El trinomio al cuadrado (o cuadrado de un trinomio) (a + b + c)² es igual al cuadrado del primer término, más el cuadrado del segundo, más el cuadrado del tercero más el doble producto del primero por el segundo, más el doble producto del primero por el tercero, más el doble producto del segundo por el tercero.
No hay que confundir el trinomio al cuadrado con el trinomio cuadrado perfecto, que es el desarrollo de un binomio al cuadrado (a + b)².
En general, el cuadrado de un polinomio (a + b + … + n)² es la suma de los cuadrados de cada uno de sus términos más los doble productos de cada término por cada uno de los términos siguientes.
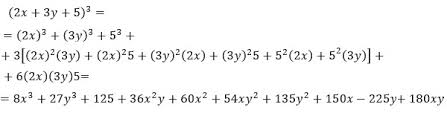
Trinomio al cubo
El trinomio al cuadrado (o cuadrado de un trinomio) (a + b + c)² es igual al cuadrado del primer término, más el cuadrado del segundo, más el cuadrado del tercero más el doble producto del primero por el segundo, más el doble producto del primero por el tercero, más el doble producto del segundo por el tercero.
No hay que confundir el trinomio al cuadrado con el trinomio cuadrado perfecto, que es el desarrollo de un binomio al cuadrado (a + b)².
En general, el cuadrado de un polinomio (a + b + … + n)² es la suma de los cuadrados de cada uno de sus términos más los doble productos de cada término por cada uno de los términos siguientes.
Diferencia de cuadrados
La diferencia de cuadrados (o resta de cuadrados) es un binomio resultado de multiplicar dos binomios conjugados, que se denominan también suma por diferencia.
A partir de una resta de cuadrados se llega a una factorización por binomios conjugados.
Binomios conjugados
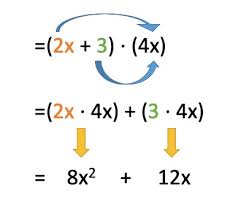
Los binomios conjugados son parejas de binomios cuyos dos términos son iguales pero difieren en que uno está unido por el signo más y el otro, por el signo menos.
Estos son ejemplos de binomios conjugados:
Al multiplicar dos binomios conjugados de la forma (a + b)(a – b), el resultado es:
El desarrollo de la diferencia de cuadrados se basa en la propiedad distributiva de la multiplicación: